Fisikastudycenter.com- Contoh Soal dan Pembahasan tentang Titik Berat Benda, Materi Fisika Kelas 2 SMA.
Mencakup titik berat gabungan benda berupa panjang, luasan, volume dengan beberapa contoh bentuk segitiga, persegi, persegi panjang, tabung dan kerucut pejal.
Contoh pertama tentang koordinat titik berat benda berupa panjang, dilanjutkan dengan benda luasan dan volume.

Soal No. 1
Tentukan koordinat titik berat susunan enam buah kawat tipis berikut ini dengan acuan titik 0 !

Pembahasan
Data dari soal :
l1 = 20, X1 = 20, Y1 = 10
l2 = 20, X2 = 60, Y2 = 10
l3 = 80, X3 = 40, Y3 = 20
l4 = 20, X4 = 0, Y4 = 30
l5 = 40, X5 = 40, Y5 = 40
l6 = 20, X6 = 80, Y6 = 30
Koordinat titik berat gabungan keenam kawat (X0 , Y0)


Soal No. 2
Tentukan letak titik berat bangun berupa luasan berikut dihitung dari bidang alasnya! 
Pembahasan
Data dari soal :
Benda 1 (warna hitam)
A1 = (20 x 60) = 1200
Y1 = 30
Benda 2 (warna biru)
A2 = (20 x 60) = 1200
Y2 = (60 + 10) = 70
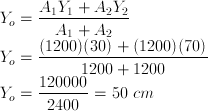
Soal No. 3
Tentukan letak titik berat bangun berikut terhadap alasnya! 
Pembahasan
Bagi bangun menjadi dua, persegi di bagian bawah dan segitiga sama kaki di bagian atas. Data :
Bidang 1 (persegi)
A1 = (90 x 90) = 8100
Y1 = 90/2 = 45
Bidang 2 (segitiga)
A2 = 1/2(90 x 90) = 4050
Y2 = 1/3(90) + 90 = 120
Letak Yo :
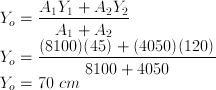
Soal No. 4
Tentukan letak titik berat bangun berikut terhadap alasnya! 
Pembahasan
Bagi bidang menjadi dua, persegi panjang yang dianggap utuh (belum dilubang) dan lubang berbentuk segitiga. Data dari soal :
Bidang 1 (Persegi panjang utuh)
A1 = (180 x 90) = 16200
Y1 = (180/2) = 90
Bidang 2 (lubang segitiga)
A2 = 1/2(90 x 90) = 4050
Y2 = 180 − (90/3) = 150
Letak Yo :

Soal No. 5
Sebuah tabung pejal disambung dengan kerucut pejal seperti pada gambar berikut! 
Tentukan letak titik berat bangun tersebut terhadap garis AB!
Pembahasan
Data :
Bangun 1 (Tabung pejal)
V1 = π r2 t = 12π r2
X1 = 6
Bangun 2 (Kerucut pejal)
V2 = 1/3 π r2 t = 4 π r2
X2 = 12 + (1/4 t) = 12 + 3 = 15
Letak Xo :
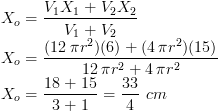
Soal Nomor 6
Karton I dan II masing-masing homogen , terbuat dari bahan yang sama dan digabung menjadi satu seperti gambar di bawah.

Tentukan koordinat titik berat benda gabungan dari titik A
(Soal Ebtanas Fisika 1988 - Essay)
- Prev
- Next >>