fisikastudycenter.com_ Naskah soal dan pembahasan olimpiade fisika tingkat kabupaten kota OSK SMA tahun 2013, 8 soal.
Soal Olimpiade Fisika OSK 2013
Soal Nomor 1
Sebuah benda bergerak pada bidang xy dengan komponen kecepatan dalam arah x dapat dinyatakan dalam bentuk ⃑vx(t) = (3t2 - 4t + 5) m/detik, t dalam detik; sedangkan komponen kecepatan dalam arah y adalah ⃑vy (t) seperti ditunjukkan dalam grafik dibawah.
Tentukanlah:
a) kecepatan benda ⃑v(t) saat t = 2 detik dan t = 4 detik.
b) percepatan benda ⃑a (t) saat t = 4 detik
c) posisi benda ⃑r (t) saat t = 9 detik, jika diketahui posisi awal benda adalah ⃑r (0) = (74i + 40j) m.

Pembahasan
a) kecepatan benda ⃑v(t) saat t = 2 detik dan t = 4 detik. Kecepatan benda ⃑v(t) diperoleh dengan menggabungkan komponen kecepatan benda dalam arah x dan dalam arah y.
Untuk t = 2 detik :
Arah x
⃑vx (t) = (3t2 - 4t + 5)
⃑vx (2) = 3(2)2 - 4(2) +5 = 9 m/s
Arah y
dari grafik diperoleh komponen kecepatan arah y saat t = 2 detik adalah 30 m/s
⃑vx (2) = 30 m/s
Sehingga
⃑v(t) = vx (t)i + vy (t)j = (9i+30j) m/s
Untuk t = 4 detik :
Arah x
⃑vx (t) = (3t2 - 4t + 5)
⃑vx (9) = 3(4)2 - 4(4) + 5 = 37 m/s
Arah y
dari potongan grafik untuk arah y

dari perbandingan segitiga kecil dan segitiga besar diperoleh untuk t = 4

b. percepatan benda ⃗a (t) saat t = 4 detik
Arah x
Percepatan diperoleh dengan menurunkan kecepatan.
vx (t) = (3t2 - 4t + 5) m/s
ax (t) = (6t - 4) m/s2
ax (4) = (6⋅4 - 4) = 20 m/s2
Arah y
Dari grafik:

Sehingga:

c) posisi benda ⃑r (t) saat t = 9 detik, jika diketahui posisi awal benda adalah ⃑r (0) = (74i + 40j) m.
Arah x
Posisi benda diperoleh dengan mengintegralkan kecepatan.

Arah y

Terlebih dahulu dicari luas-luas dari garafik v-t diatas:

sehingga, dengan yo = 40 diperoleh
y(t) = yo + Luas
y(t) = 40 + 260 = 300 m
Posisi benda saat t = 9 detik dengan demikian adalah:
⃗r (9) = 686i + 300j
Soal Nomor 2
Seseorang (massa 60 kg) terikat dan terhubung ke sebuah sistem katrol sebagaimana tampak pada gambar di samping. Katrol dan tali dianggap tak bermassa dan licin.

Jika percepatan gravitasi dianggap 10 m/det2, tentukan gaya yang harus diberikan oleh orang tersebut ke tali agar ia bisa mempertahankan dirinya untuk tidak menyentuh lantai.
Pembahasan
Gaya-gaya yang bekerja pada sistem di atas adalah

T2, T3, T4 akan sama besar (satu tali, katrol licin).
T2 = T3 = T4 = T
Tinjau katrol pertama yang bawah, berlaku kesetimbangan berikut:
T1 = T3 + T4
T1 = T + T
T1 = 2T
Tinjau orang
w = T1 + T2
600 = 2T + T
600 = 3T
T = 200 N
Pada tangan orang dan tali terjadi aksi-reaksi. Tangan orang menarik tali dengan gaya F = 200 N, dan tali menarik tangan orang dengan gaya T = 200 N.
Soal Nomor 3
Sebuah balok (massa m) bergerak dengan kelajuan awal νo di atas lantai licin. Sebuah batang homogen bermassa M ( M > m) dan panjangnya L tergantung dengan bebas pada langit-langit dan mula-mula diam (lihat gambar di bawah). Batang M ditumbuk oleh balok m tersebut. 
Tepat setelah tumbukan, batang berayun dan balok diam.
a) Periksalah apakah kasus di atas termasuk tumbukan elastik atau tak-elastik.
b) Tentukan tinggi maksimum batang homogen berayun.
Pembahasan
Pada kasus ini berlaku hukum kekekalan momentum angular. Dimana momentum angular (momentum sudut) adalah L = mvr atau L = Iω . Sebelum tumbukan momentum angularnya praktis dari balok saja, karena batang diam. Setelah tumbukan, balok diam sementara itu batang berputar dengan kecepatan sudut ω . Perhatikan gambar. 
Dari teorema sumbu sejajar untuk mencari momen inersia batang akan didapat poros di ujung momen inersianya adalah 1/3 ML2. Dari kekekalan momentum sudut diperoleh kecepatan sudut batang setelah tumbukan. 
Berikutnya periksa apakah Energi kinetik sebelum tumbukan dan setelah tumbukan tetap atau terjadi perubahan. 
karena nilai (3m/M) lebih kecil dari 1, maka terlihat bahwa Ek’ lebih kecil dari Ek, artinya terdapat hilang energi kinetik, sehingga tumbukan bersifat tak-elastik.
Sesaat setelah tumbukan energi kinetik yang dimiliki batang adalah Ek', dan saat berhenti sebelum kemudian berayun lagi ke bawah, energi ini telah diubah menjadi energi potensial untuk mencapai ketinggian h. 
Soal Nomor 4
Dua buah pegas identik, masing-masing dengan konstanta pegas k, terhubung dengan sebuah massa m dalam posisi mendatar (lihat gambar dibawah).

Kedua ujung pegas diikatkan ke dinding agar tidak terlepas. Dalam posisi diam/setimbang, jarak benda m ke masing-masing dinding adalah d.
(a) Tunjukkan apakah pada sistem pegas tersebut dimungkinkan benda m mengalami gerak osilasi harmonik sederhana pada arah vertikal?
(b) Jika jawaban pada pertanyaan (a) di atas adalah ya, tentukanlah frekuensinya.
Pembahasan
Gaya-gaya yang bekerja pada sistem dengan pengabaian gravitasi adalah sebagai berikut: 
Saat massa m disimpangkan ke bawah sejauh Δy, sudut yang terbentuk antara masing-masing pegas adalah θ, dimana θ relatif kecil. F adalah gaya dari masing-masing pegas. Besar dari gaya pemulih yang bekerja pada m adalah: 
Dengan asumsi θ relatif kecil maka diperoleh hubungan: 
gaya pemulih di atas bisa diekspresikan sebagai 
Menentukan gaya masing-masing pegas (F) Panjang pegas mula-mula adalah d1 = d, kemudian saat disimpangkan panjangnya menjadi d2 dimana dari gambar di atas diperoleh hubungan 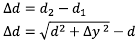
Kembali ke gaya pemulih tadi, dengan memasukkan gaya pegasnya: 
Untuk menyederhanakan bentuk dalam kurung dengan bantuan binomial newton :
potong hingga 2 suku terdepan saja: 
Terlihat gaya pemulih pada sistem sebanding dengan simpangannya sehingga dimungkinkan terjadinya SHM.
b) Frekuensi osilasi

Catatan:
Pengambilan set-up awal yang berbeda, dapat menghasilkan format jawaban yang lain seperti penggunaan gravitasi dan beda pengambilan pertambahan panjang pegas, namun intinya sama yaitu bagaimana agar mendapatkan gaya pemulih yang sebanding dengan simpangannya sebagai syarat simple harmonic motion (SHM) atau gerak harmonik sederhana (GHS).
Soal Nomor 5
Bola biliar dengan jari-jari r, massa m dan momen inersia I berada di atas meja biliar. Bola disodok dengan gaya horizontal, sehingga bergerak menggelinding ke kanan tanpa slip dengan kecepatan u. 
Bola kemudian mengenai dinding meja billiar yang memiliki ketinggian tepi h seperti ditunjukkan pada gambar. Akibatnya lalu bola itu berbalik menggelinding tanpa slip dengan kecepatan v. Tentukanlah hubungan antara h dan r agar kondisi ini terjadi. Anggap bola mengenai tepi meja dengan arah normal.
Pembahasan
Bola setelah menumbuk meja. Dengan pendekatan torsi, ada gaya yang bekerja hingga bola menggelinding balik ke kiri. 
Gaya F bekerja pada jarak d dari pusat bola, dimana h = d + r atau d = h – r. Gaya F diambil dari gaya impuls, adanya perubahan kecepatan bola dari v1 = u, menjadi v2 = v. 
Bola menggelinding tanpa slip, sehingga berlaku: 
diperoleh hubungan antara h dan r dimana h = 7/5 r
(Jika dihitung dengan menampilkan gaya gesek f di dasar bola, akan mendapatkan hasil yang sama.)
Gaya-gaya, termasuk gesekan 
Dari ΣF = ma
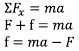
Dari ΣΤ 
Substitusi 
Soal Nomor 6
Sebuah bola dengan radius r menggelinding secara horizontal tanpa slip pada dua buah rel sejajar yang berjarak r/2. Bola menggelinding tegak lurus terhadap bidang kertas (perhatikan gambar samping).

a. Gambarkan kondisi tersebut dalam tampak depan dan tampak samping. Tentukan titik manakah (pada bola) yang memiliki kecepatan sesaat maksimum !
b. Cari besarnya kecepatan maksimum diatas jika pusat massa bola memiliki kelajuan v !
Pembahasan
a) Gambar kondisi tampak depan dan tampak samping.

tampak dari depan

Tampak dari samping
Semakin jauh jarak titik dari poros rotasi sesaat, kecepatannya semakin besar. Kecepatan sesaat paling besar di titik C, yang paling jauh dari poros rotasi sesaat.
b) Besarnya kecepatan maksimum jika pusat massa bola memiliki kelajuan v
Terlebih dahulu mencari jarak titik C dari titik A, cari d dulu:

diperoleh panjang d

Jadi jaraknya titik C dari A, adalah d + r. Berikutnya dengan pendekatan rumus yang biasa dipakai pada hubungan roda-roda, dimana titik B dan titik C memiliki ω yang sama saat A menjadi poros sesaat. Diingat hubungan ω dengan v dan r adalah ω = v / r

atau dengan format akhir yang lain sbb:

Soal Nomor 7
Suatu bola bermassa m dan berjari-jari r menggelinding tanpa slip pada permukaan setengah bola yang kasar dan berjari-jari R (R > r) seperti tampak pada gambar di bawah ini.

a. Jika bola m mula-mula diam di titik A dan kemudian menggelinding ke bawah pada permukaan setengah bola, maka tentukan kelajuan bola tersebut pada titik terendah.
b. Bila bola tersebut dalam geraknya di bagian a) di atas, ia berosilasi di sekitar titik terendah, tentukan periode osilasi tersebut!
Pembahasan
a) kelajuan bola di titik terendah

Dengan kekekalan energi mekanik ambil titik C (h = 0) dan titik A (h = R - r), di sini bolanya dianggap bola pejal.

Gaya pemulih yang bekerja pada bola adalah:
Frestoring = mg sin θ − f
Dari gerak rotasi bola kecil, tidak slip, Στ = Iα
Sehingga gaya pemulihnya:

Dari 
didapat 
Untuk sudut simpang kecil, harga sin θ mendekati θ dan x = θ (R - r).
Sehingga: 
Soal Nomor 8
Lokomotif mainan (massa mL) bergerak pada lintasan melingkar horizontal berjari-jari R dan bermassa total mT. Lintasan berbentuk pelek dari sebuah roda tak bermassa yang dapat bebas berotasi tanpa gesekan terhadap sumbu/poros vertikal. 
Lokomotif mulai bergerak dari keadaan diam dan dipercepat tanpa slip sampai mencapai kecepatan akhir v relatif terhadap lintasan. Hitunglah kecepatan akhir lokomotif, vf, relatif terhadap lantai.
Pembahasan
Data soal:
mL = massa loko
mT = massa pelek
v = kecepatan relatif loko terhadap lintasan (pelek).
vf = kecepatan akhir loko terhadap lantai (tanah).
Berhubungan dengan kecepatan relatif, disini akan digunakan dulu lambang-lambang:
vlp untuk kecepatan relatif loko terhadap pelek
vlt untuk kecepatan relatif loko terhadap tanah
vpt = kecepatan relatif pelek terhadap tanah
Kembali ke soal diatas, hukum kekekalan momentum sudut (L) diberlakukan untuk kasus ini, loko dan pelek mula-mula diam (kecepatan nol), kecepatan sudut akhir masing-masing ωl dan ωp.
Hukum kekekalan momentum sudut sistem lokomotif dan pelek sebagai lintasan. 
Momen inersia loko I = mr2 dan untuk pelek anggap silinder tipis berongga, hingga momen inersianya I = mr2 juga. 
Berikutnya dari data soal v = kecepatan relatif loko terhadap lintasan (pelek). 
Gabungkan (i) dan (ii) 
Di soal, vlt dinyatakan sebagai vf, massa loko ml sebagai mL, dan massa pelek mp sebagai mT, sehingga jika ikut lambang-lambang soal diperoleh 