- Details
- Category: Materi Fisika SMA
Materi : Listrik Statis
Topik : Menentukan Potensial Suatu Titik di Sekitar Beberapa Muatan Listrik
Kelas : 12 SMA IPA
Author : Fisika Study Center
(Beginner Level )
Rumus Potensial Listrik
 |
dimana
V = potensial listrik suatu titik (volt = V)
r = jarak titik dari muatan listrik (meter = m)
q = besar muatan listrik (coulomb = C)
Tanda Plus dan Tanda Minus pada Muatan
Tanda plus dan minus pada muatan diikutkan dalam perhitungan, jadi tidak seperti waktu menghitung gaya coulomb dan kuat medan listrik kemarin dimana semua dimasukkan positif (Potensial listrik (V) dan energi potensial listrik (Ep) adalah besaran skalar, gaya coulomb (F) dan kuat medan listrik (E) termasuk besaran vektor!!)
Cermati contoh soal berikut:
Titik P diantara empat muatan masing-masing + 2 C, − 4 C, + 5 C dan −6 Coulomb seperti terlihat pada gambar berikut.

Tentukan potensial listrik di titik P!
Jarak masing-masing muatan ke titik yang akan dicari potensial listriknya sudah tersedia, tinggal lanjut saja
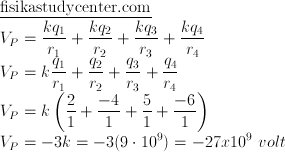
Besar sekali hasilnya? Sekedar contoh perhitungan dengan angka-angka yang dipermudah.
prep. by Fisika Study Center
- Details
- Category: Materi Fisika SMA
Materi : Listrik Statis
Topik : Gaya Coulomb Muatan-Muatan Segaris
Kelas : 12 SMA IPA
Author : Fisika Study Center
(Beginner)
Dua buah muatan yang berada pada jarak r akan saling tarik-menarik atau tolak menolak, tergantung pada jenis muatannya.
Untuk muatan sejenis, positif-positif atau negatif-negatif akan saling tolak, untuk muatan berlawan jenis,
negatif-positif atau positif-negatif akan saling tarik.
Gaya tarik atau tolak tersebut dikenal dengan istilah gaya
listrik atau gaya Coulomb.
Formulasi seperti berikut:
 |
dimana
F = gaya coulomb (N)
q1 = besar muatan pertama (C)
q2 = besar muatan kedua (C)
r = jarak pisah muatan pertama dan kedua (m)
k = konstanta gaya listrik = 9 x 109 N m2 C−2
jika diperlukan
k = 1/4π εo
dimana εo = 8,85 x 10−12 C2 N−1 m−2
Untuk dicatat gaya listrik dan kuat medan listrik termasuk besaran vektor sehingga mengingat kembali materi vektor sangat diperlukan disini.
Pelajari contoh-contoh dasar berikut, dengan catatan angka-angka sengaja dipermudah untuk menyederhanakan perhitungan, sehingga hasil-hasil akan jauh dari faktual keseharian:
Tanda Plus Minus
→ Diberikan 2 buah muatan qA = + 3 C dan qB = −6 C terpisah sejauh 3 m. Tentukan besar gaya listrik yang terjadi!
Data data dari soal diatas:
q1 = qA = + 3C
q2 = qB = −6 C
r = 3 m

ke mana tanda plus minusnya?! untuk menghitung F dan E tanda plus minus tak perlu diikutkan lagi, kita tahu arah gaya-gayanya yaitu muatan A ditarik ke arah B dan muatan B ditarik ke arah A karena berlawan tanda, karena plus minusnya tadi. untuk perhitungan2 berikutnya cermati arah-arah gaya yang dihasilkan alih-alih tanda plus minus yang dihilangkan seperti contoh berikutnya:
Interaksi Muatan Lebih dari Dua dan Segaris
→ 4 buah muatan seperti gambar berikut:

Tentukan besar gaya akibat akibat interaksi muatan-muatan tersebut pada muatan yang paling kanan!
Muatan keempat, paling kanan dipengaruhi oleh 3 muatan lainnya, muatan I, II dan III. Temukan dulu gaya antara muatan keempat dan 3 muatan lainnya secara terpisah, simpan dulu nilai k.
Muatan IV dan III, dengan jarak 1 m:
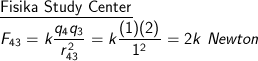
Arah gaya adalah ke kiri.
Muatan IV dan II, dengan jarak 2 m:
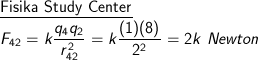
Arah gaya adalah ke kiri.
Muatan IV dan I, dengan jarak 3 m:

Arah gaya adalah ke kanan.
Berikut ilustrasi arah arah gaya coulomb pada muatan keempat:

Jumlah gaya ke arah kanan adalah 2k, jumlah gaya ke arah kiri adalah 2k + 2k = 4k, gaya total:
F = 4k − 2k = 2k Newton = 2 (9 x 109) = 18 x 109 Newton arah ke kiri.
prep. by Fisika Study Center
- Details
- Category: Materi Fisika SMA
Materi : Listrik Statis
Topik : Menentukan Letak Titik dengan Kuat Medan Listrik Nol
Kelas : 12 SMA IPA
Author : Fisika Study Center
(Beginner)
Dengan asumsi bahwa adik-adik tidak bingung dalam menentukan arah medan listrik (muatan positif arah keluar, muatan negatif arah masuk dan seterusnya, kalo masih liat aja di contoh Listrik Statis 12 nomor 6), disini akan diambil kesimpulan dari beberapa kasus menentukan letak titik yang kuat medan listriknya nol.
Dua muatan sama tanda
Muatan (+) dengan (+) atau muatan (−) dengan (−), maka daerah nol berada di antara kedua muatan (antara A dan B, tidak akan di kiri A, atau di kanan B).
Letak titik nol akan lebih dekat ke muatan yang nilainya lebih kecil. Kalau sama besar, seperti gambar di atas,, ya pas ditengah-tengah.
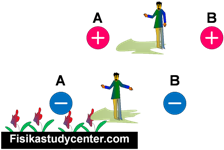
Dua muatan beda tanda
Muatan (+) dengan muatan (−) atau muatan (−) dengan (+), daerah nol akan di kiri A atau di kanan B, seperti tadi, akan dekat ke muatan yang nilainya lebih kecil (tanpa melihat plus minusnya). Cermati 4 variasi berikut!




Atau kalau tak mau pusing dengan kesimpulan-kesimpulan tadi, langsung saja coba dicari seperti contoh berikut:
Muatan A + 9 C dan muatan B −16 C terpisah sejauh 1 meter seperti gambar berikut. Tentukan letak titik C, dimana kuat medan listrik sama dengan nol!

Seperti telah disimpulkan di atas, letak titik nol ada di kiri A, karena beda tanda dan 9 lebih kecil dari 16. Misal jarak C adalah x dari A, rA = x dan rB = 1 + x

diperoleh jawaban

Hasilnya positif, sehingga memang benar C di kiri A sejauh 3 meter
Kita coba cari dari tempat lain yaitu dari kanan B, sehingga rA = 1 + x dan rB = x

diperoleh jawaban

Hasilnya negatif 4, artinya dari muatan B bukan ke kanan 4 m, tetapi ke kiri sejauh 4 m, atau 3 m juga di kiri muatan A seperti perhitungan sebelumnya.
prep. by Fisika Study Center
- Details
- Category: Materi Fisika SMA
Materi : Gravitasi
Topik : Menentukan Percepatan Gravitasi (Bumi atau Planet-Planet) pada Dua Tempat Berbeda Tinggi
Kelas : XI SMA IPA
Author : Fisika Study Center
(Beginner)
Rumus Percepatan Gravitasi
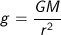 |
Dimana
g = kuat medan gravitasi atau percepatan gravitasi (N/m) atau (m/s2)
r = jarak titik ke pusat massa (pusat bumi atau pusat planet) [m]
G = konstanta gravitasi = 6,67 x 10−11 kg−1 m3 s−2
M = massa penghasil kuat medan gravitasi (massa bumi atau massa planet) [kg]
Membandingkan Percepatan Gravitasi untuk Dua Titik yang berbeda Jarak
Dua tempat yaitu 1 dan 2 diatas permukaan suatu planet (atau bumi). Perhatikan gambar berikut
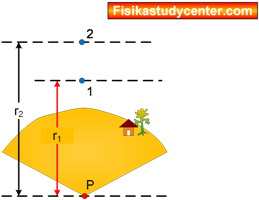
Dua tempat yang berbeda jarak dari pusat massa akan memiliki kuat medan gravitasi yang berbeda, sehingga berat suatu benda akan berlainan pula jika diukur pada dua tempat tersebut. Dari default rumus di atas jika dibuatkan perbandingan
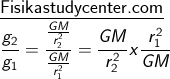
 |
Menentukan Percepatan Gravitasi suatu Titik dengan Acuan Titik lain yang Diketahui Nilai Percepatan Gravitasinya
Bila salah satu titik / tempat (tempat pertama) telah diketahui nilai percepatan gravitasinya maka dengan mudah percepatan gravitasi untuk tempat kedua adalah
 |
Ikuti contoh-contoh soal berikut:
→Titik pertama dan kedua berada di permukaan suatu planet dengan jarak-jarak yang diketahui diukur dari permukaan planet, perhatikan gambar berikut!

Tentukan nilai perbandingan percepatan gravitasi planet tersebut pada titik kedua dan pertama jika jari-jari planet tersebut sebesar R!
Pembahasan
Data dari soal :
r1 = R + 1/2 R
r2 = R + 1/2 R + 1/4 R

→Perhatikan gambar berikut!

Jika percepatan gravitasi di permukaan bumi adalah 10 m/s2 tentukan percepatan gravitasi bumi pada tempat 2, R adalah jari-jari bumi!
Pembahasan
Data dari soal :
r1 = R
r2 = R + 2R

Kesimpulan:
-Semakin jauh suatu titik dari pusat massa (bumi, planet) percepatan gravitasi atau kuat medan gravitasinya semakin kecil.
-Kuat medan gravitasi pada suatu titik dipegaruhi oleh jarak titik ke pusat massa, dan oleh massa penghasil medan gravitasi (bumi, planet, bulan dll)
-Konsisten dengan pengambilan jarak titik, yaitu dari pusat (pusat bumi, pusat planet,..)
prepared by :
fisikastudycenter.com
- Details
- Category: Materi Fisika SMA
Materi : Gravitasi
Topik : Menentukan Kelajuan Lepas (Escape Speed) dan Kelajuan Satelit
Kelas : XI SMA IPA
Author : Fisika Study Center
(Beginner)
Kelajuan Lepas
Pada umumnya benda yang dilemparkan ke atas akan jatuh kembali ke bumi.
Ada nilai kelajuan awal tertentu yang membuat benda dilempar / ditembakkan ke atas dari permukaan bumi agar tidak kembali lagi.
Kelajuan tersebut dikenal dengan istilah kelajuan lepas (Escape speed/escape velocity), yang didapatkan dengan penggunaan hukum kekekalan energi.
 |
Dimana
R = jari-jari bumi [m]
G = konstanta gravitasi = 6,67 x 10−11 kg−1 m3 s−2
M = massa bumi [kg]